What Do Error Bars Show? They are a powerful tool for visualizing the uncertainty and variability in data. By understanding how to interpret error bars, you can gain valuable insights into the significance and reliability of your findings.
Error bars represent the range of possible values for a given data point. They help you assess the precision and accuracy of your measurements and determine whether differences between data points are statistically significant.
Definition and Purpose of Error Bars
Error bars are graphical representations of the variability or uncertainty associated with data points in a data visualization. They provide a visual indication of the range within which the true value of the data point is likely to fall.
Error bars can be calculated using various statistical methods, such as:
- Standard deviation: A measure of the spread of data around the mean.
- Standard error of the mean (SEM): A measure of the variability of the mean of a sample.
Error bars are used in data analysis to convey the uncertainty associated with the data points. This helps in understanding the significance of the results and making informed decisions.
Interpreting Error Bars
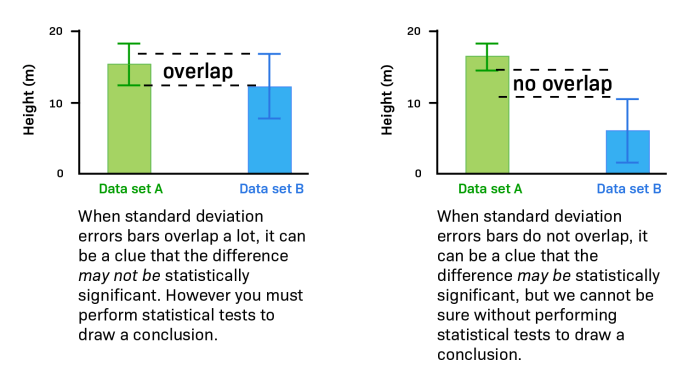
Error bars provide a visual representation of the uncertainty associated with data points. By interpreting the range and magnitude of error bars, researchers can draw meaningful conclusions about the data and determine the significance of differences between data points.
Range and Magnitude
The range of an error bar represents the variability or spread of the data. A wider error bar indicates greater variability, while a narrower error bar indicates less variability. The magnitude of an error bar, measured by its length, represents the amount of uncertainty associated with the data point.
Significance of Differences
Error bars can help determine the significance of differences between data points. If the error bars of two data points do not overlap, it suggests that the difference between the data points is statistically significant. Conversely, if the error bars overlap, it indicates that the difference may not be statistically significant.
Limitations of Error Bars
While error bars are a useful tool for visualizing uncertainty, they have certain limitations. Error bars only represent the uncertainty associated with the data point itself and do not account for other sources of uncertainty, such as sampling error or measurement error.
Additionally, error bars may not be reliable if the data is not normally distributed.
Types of Error Bars: What Do Error Bars Show
Error bars represent the variability or uncertainty associated with a measurement or estimate. Different types of error bars convey different information about the data and have different underlying assumptions.
The most common types of error bars are:
Standard Deviation
Standard deviation measures the spread or dispersion of data. It represents the average distance of data points from the mean. The larger the standard deviation, the more spread out the data is.
Error bars graphically represent the variability of data, conveying the degree of uncertainty associated with a measurement. Like the lamentations over a deceased beloved in the Wailed Over Dead Crossword Clue , error bars depict the range of possible values, allowing us to assess the reliability of our conclusions.
They serve as essential tools in scientific research, helping us to understand the significance and limitations of our findings.
Standard deviation = √(Σ(x
Error bars illustrate the range of possible values within a data set, providing a visual representation of uncertainty. While this concept is crucial for understanding data analysis, it’s equally important to explore the latest home design trends at the upcoming Melbourne Home Show 2024 . This renowned event showcases innovative ideas and products for home improvement, offering valuable insights into enhancing your living space.
By understanding error bars and attending the Home Show, you’ll gain a comprehensive understanding of data analysis and modern home design.
μ)² / N)
Where:
- x is the data point
- μ is the mean
- N is the number of data points
Standard Error of the Mean
Standard error of the mean (SEM) measures the variability of the sample mean. It represents the standard deviation of the distribution of sample means that would be obtained if the experiment were repeated multiple times.
SEM = Standard deviation / √N
Where:
- Standard deviation is the standard deviation of the sample
- N is the sample size
Confidence Intervals
Confidence intervals provide a range of values within which the true population mean is likely to fall. They are calculated using a specified level of confidence, typically 95% or 99%.
Confidence interval = Mean ± (z-score
Error bars are used to show the amount of uncertainty in a measurement. This can be important in understanding the reliability of a result. As Neil deGrasse Tyson writes in his book “We Were Born To Inherit The Stars” , “The greatest adventure is the one that lies ahead.”
This is true in science as well, where we are constantly learning and refining our understanding of the world around us. Error bars help us to understand the limits of our knowledge and to appreciate the complexity of the universe.
SEM)
Where:
- Mean is the sample mean
- z-score is the critical value from the standard normal distribution corresponding to the desired confidence level
- SEM is the standard error of the mean
Using Error Bars Effectively
To use error bars effectively, it’s crucial to choose the appropriate type for the data and present them clearly to avoid misinterpretation.
Choosing the Right Type of Error Bar
The choice of error bar type depends on the nature of the data:
- Standard Error Bars:Represent the standard deviation of the data and are suitable for normally distributed data.
- Standard Error of the Mean (SEM):Represent the standard error divided by the square root of the sample size and are used when comparing means between groups.
- Confidence Intervals:Represent a range of values within which the true mean is likely to lie and are used when the sample size is small or the data is non-normal.
Presenting Error Bars in Charts and Graphs
When presenting error bars, it’s important to:
- Use a clear and consistent format.
- Label the error bars appropriately (e.g., standard error, confidence interval).
- Ensure the error bars are visible and easy to interpret.
Avoiding Misinterpreting Error Bars, What Do Error Bars Show
To avoid misinterpreting error bars, it’s crucial to:
- Understand the type of error bar used and its statistical significance.
- Consider the sample size and the variability of the data.
- Avoid drawing conclusions based solely on the presence or absence of error bars.
Applications of Error Bars

Error bars are a versatile tool used in various fields to represent uncertainty and variability in data. They provide a visual representation of the range within which the true value of a measurement is likely to fall.
Scientific Research
In scientific research, error bars are used to indicate the uncertainty associated with experimental measurements. This uncertainty can arise from various sources, such as measurement errors, sample variability, or instrument limitations. By including error bars in graphs and charts, researchers can convey the reliability of their findings and the level of confidence they have in their conclusions.
Business Analysis
Error bars are also used in business analysis to represent uncertainty in forecasts, projections, and estimates. For example, a financial analyst might use error bars to indicate the range of possible outcomes for a company’s revenue or profit. This information can help businesses make more informed decisions by considering the potential variability in their predictions.
Medical Studies
In medical studies, error bars are used to show the variability in patient outcomes or the uncertainty associated with treatment effects. For instance, a clinical trial might report the average improvement in a patient’s condition, along with error bars that indicate the range of individual responses to the treatment.
This information helps clinicians understand the potential benefits and risks of different treatments and make more informed decisions about patient care.
Final Review
In conclusion, error bars are an essential tool for data analysis. They provide valuable information about the uncertainty and variability in your data, allowing you to make more informed conclusions and avoid misleading interpretations.
Popular Questions
What is the purpose of error bars?
Error bars show the range of possible values for a given data point, helping you assess the precision and accuracy of your measurements.
How do I interpret error bars?
Error bars are typically displayed as a vertical line extending above and below a data point. The length of the line represents the range of possible values, and the center of the line represents the mean or median value.
When should I use error bars?
Error bars should be used whenever you are presenting data that has some degree of uncertainty or variability.